Hai sobat Belajar Mtk pada kesempatan ini kita akan membahas Rumus Volume Balok Dan Luas Permukaan Balok . Salah satu bentuk bangun ruang yang pasti akan masuk dalam pembahasan pelajaran matematika di sekolah adalah balok. Dalam kehidupan sehari-hari bangun berbentuk balok juga bisa dengan mudah kita temukan bahkan sering kita gunakan dalam aktivitas. Sebagai contoh mudah adalah kotak tempat makanan yang sering kita gunakan.
Selain balok di dalam matematika juga dikenal bangun ruang yang disebut dengan kubus. Meskipun seperti sama sebenarnya balok dan kubus itu berbeda.
A. Perbedaan Balok dan Kubus
- Balok
Balok merupakan sebuah bangun ruang yang terdiri dari 6 sisi dimana rusuk-rusuknya panjang dan lebarnya berbeda. Atau bisa dikatakan balok adalah persegi panjang yang memiliki volume.
Perbedaan balok dengan kubus adalah pada ukuran sisinya atau panjang dan lebarnya. Jika balok merupakan persegi panjang dimana sisi panjang dan lebarnya berbeda ukuran maka pada kubus panjang semua sisinya sama.
B. Unsur Balok dan Kubus
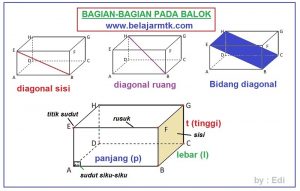
- Sisi yaitu bidang yang menjadi batas pada bangun ruang terdiri dari sisi tegak dan sisi datar.
- Rusuk yaitu sebuah garis yang merupakan perpotongan antara 2 sisi bidang kubus atau balok.
- Titik Sudut merupakan titik dimana 3 rusuk yang saling berdekatan bertemu.
- Diagonal yaitu garis penghubung antara 2 sudut pada titik sebidang di dalam kubus atau balok.
- Bidang Diagonal merupakan bidang yang terdapat pada kubus atau balok dan melalui 2 rusuk yang sejajar tetapi tidak sebidang atau tidak dalam 1 sisi.
C. Sifat atau ciri-ciri balok
- Memiliki 8 titik sudut, yaitu titik sudut A, B, C, D, E, F, G dan H
- Memiliki 6 bidang sisi, yaitu sisi ABCD, EFGH, ABFE, DCGH, BCGE dan ADHE
- Memiliki 12 rusuk, yaitu rusuk : AB, BF, FE, EA, DC, CG, GH, HD, EH, FG, AD dan BC
- Mempunyai 4 diagonal ruang dan 12 diagonal bidang.
- Semua sudut berbentuk siku-siku
Setelah membahas secara singkat apa itu balok dan perbedaannya dengan kubus lengkap dengan unsur yang ada di dalamnya selanjutnya akan dibahas tentang rumus-rumus dalam hitungan matematika.
Dibawah ini akan kita bahas tentang rumus volume balok dan luas permukaan balok lengkap contoh soalnya. Dengan adanya contoh berikut diharapkan akan membantu para siswa untuk lebih mudah memahami dan mengerti tentang bangun ruang balok pada khususnya.
D. Rumus Balok
1 . Rumus Volume Balok
Menghitung volume balok sama artinya dengan menghitung berapa isi dari balok tersebut. Dalam menghitung volume atau isi balok maka kita harus mengetahui berapa panjang, lebar dan tinggi dari sisi balok tersebut. Bagian-bagian mana saja yang disebut sebagai panjang, lebar dan tinggi bisa dilihat pada gambar di atas.
Adapun cara atau rumus dalam menghitung berapa volume dari balok adalah sebagai berikut :
Volume Balok = panjang x lebar x tinggi
atau
V = p x l x t
Karena pada judulnya telah disebutkan bahwa dalam artikel ini akan dibahas tentang rumus volume balok dan luas permukaan balok lengkap contoh soalnya jadi setelah kita mengetahui bagaimana menghitung volume juga akan dijelaskan tentang luas permukaan balok.
Sebagaimana bangun ruang pada umumnya tentu saja balok memiliki luas pada permukaannya. Inilah yang akan dibahas selanjutnya dibawah ini.
Balok memiliki 6 sisi bidang dan untuk mengetahui berapa luas permukaan totalnya artinya kita harus menjumlahkan semua luas bidang yang ada.
Baca juga : Rumus Volume Tabung dan Luas Permukaannya
2. Rumus Luas Permukaan Balok
Untuk menghitung berapa luas permukaan pada balok maka caranya adalah dengan menghitung luas dari setiap persegi panjang pada balok tersebut.
Rumus luas persegi panjang
L= panjang (p) x lebar (l)
Jadi untuk mengetahui berapa luas permukaan balok secara keseluruhan kita harus menghitung terlebih dahulu masing-masing luas dari persegi panjang 1,2,3,4,5 dan 6 seperti contoh gambar di bawah.
Rumus Luas Permukaan Balok
Karena balok mempunyai 6 sisi atau mempunyai 3 pasang sisi persegi panjang kongruen atau sama besar, maka untuk mencari luas permukaannya yaitu
L permukaan = 2 L1 + 2 L2 + 2 L5
L permukaan = 2 (L1 + L2 + L5)
L = 2 (pt + pl + lt)
E. Contoh soal :
Contoh soal 1
Sebuah balok memiliki ukuran sebagai berikut panjang 10 meter, lebar 3 meter dan tinggi 5 meter. Berapakah isi atau volume dari balok tersebut?
Jawaban :
Sesuai dengan rumus yang sudah dituliskan di atas maka cara menghitung volume balok adalah dengan mengalikan panjang, lebar dan tinggi yang terdapat pada bangun ruang tersebut. Untuk soal di atas maka perhitungan dari volume atau isinya adalah sebagai berikut :
panjang : 10 meter, lebar : 3 meter, tinggi : 5 meter
Volume : 10 x 3 x 5 = 150 m3
Jadi isi atau volume dari balok tersebut adalah sebesar 150 meter kubik (m3).
Contoh soal 2
Sebuah balok dengan ukuran panjang 10 meter dan lebar 3 meter serta tinggi 5 meter, hitunglah berapa luas permukaannya.
Diketahui :
p = 10 m
l = 3 m
t = 5 m
Ditanyakan = Luas Permukaan Balok (L) ?
L = 2 (pl + pt + lt)
L = 2 (10*3 + 10*5 + 3*5)
L = 2 (30 + 50 +15)
L = 2 (95) = 190 m3
Contoh soal 3
Sebuah akuarium berbentuk balok dengan ukuran panjang 2 m kemudian lebarnya 1 m kemudian tingginya 1 m hitung berapa volume dan luas permukaan akuarium tersebut?
Jawab :
Diketahui :
p = 2 m
l = 1 m
t = 1 m
Ditanyakan = Volume (V) dan Luas Permukaan (L) ?
V = p x l x t
V = 2 m x 1 m x 1m = 2 m3
L = 2 (pl + pt + lt)
L = 2 (2*1 + 2*1 + 1*1)
L = 2 (2 + 2 +1) = 10 m2
Jadi Volume dan Luas permukaan akuarium tersebut adalah 2 m dan 10 m?
Contoh soal 4
Sebuah balok memiliki volume sebesar 500 cm, kemudian tingginya adalah 2cm sedangkan lebarnya adalah 10 cm, berapakah Panjang balok tersebut ?
Jawab :
Diketahui :
V = 500 cm3
l = 10 cm
t = 2 cm
Ditanyakan = Panjang Balok (p) ?
V = p x l x t
p = V / (l xt)
p = 500 / (10 x2)
p = 500 / 20 = 25 cm
Jadi Panjang balok tersebut adalah 25 cm
Berikut kumpulan rumus-rumus balok
| Ditanyakan | Rumusnya | Keterangan |
| Volume | V = p x l x t | |
| Luas Permukaan | L = 2 (pl + pt + lt) | |
| Panjang | p = V / l x t | diketahui V |
| p =(L/2 – lt)/(l + t) | diketahui L | |
| Tinggi | t = V / p x l | diketahui V |
| t =(L/2 – pl)/(p + l) | diketahui L | |
| Lebar | l = V / p x t | diketahui V |
| l =(L/2 – pt)/(p + t) | diketahui L | |
| Diagonal bidang | db =√ a2+b2 | |
| Diagonal ruang | dr =√ p2 + l2 + t2 |
Berikut kalkulator hitung Luas balok dan Keliling balok, silahkan dicoba.
Baca juga : Rumus Volume Kerucut dan Luas Permukaannya
Demikian penjelasan tentang rumus volume balok dan luas permukaan balok lengkap contoh soalnya semoga bisa dipahami.