Rumus Pencerminan terhadap Garis y=x dan Contoh Soalnya

Hai sobat Belajar MTK – Salah satu materi pelajaran matematika SMA kelas XII yang perlu dikuasai adalah rumus pencerminan terhadap garis y=x dan contoh soalnya. Materi ini termasuk dalam ilmu geometri, khususnya dalam pembahasan tentang transformasi geometri. Untuk mempermudah pemahaman tentang materi ini, Kalian harus terlebih dahulu menguasai materi tentang fungsi, trigonometri, dan matriks.

A. Pengertian dan Jenis Transformasi Geometri

Jika diamati, banyak contoh fenomena transformasi geometri yang bisa Kalian temukan dalam kehidupan sehari-hari. Dalam melakukan aktivitas keseharian, manusia tidak bisa dilepaskan dari aktivitas bergerak. Berjalan, berlari, melompat, atau aktivitas bergerak lainnya mengakibatkan terjadinya perubahan posisi atau tempat. Inilah salah satu contoh fenomena transformasi dalam kehidupan sehari-hari.

Lalu, apa yang dimaksud dengan transformasi geometri? Transformasi geometri adalah perubahan yang terjadi pada suatu bidang geometri dari posisi, ukuran, atau bentuk awal ke posisi, ukuran, atau bentuk yang lain. Perubahan tersebut tidak terjadi secara sebarang, tetapi ada aturan atau rumus tertentu yang membuat sebuah objek mengalami perubahan.

Berdasarkan perubahannya, terdapat empat macam transformasi geometri, yaitu:

• Translasi atau pergeseran
• Refleksi atau pencerminan
• Rotasi atau perputaran
• Dilatasi atau perkalian

Apabila hasil perubahannya bersifat kongruen (sama dan sebangun) terhadap bidang yang ditransformasikan, transformasinya disebut transformasi isometri. Transformasi isometri ini terbagi dalam dua jenis, yaitu transformasi isometri langsung dan berhadapan. Transformasi isometri langsung dapat berupa translasi atau rotasi, sedangkan yang tergolong transformasi berhadapan adalah refleksi atau pencerminan.

Dalam tulisan ini, Kalian akan mempelajari salah satu jenis ilmu transformasi geometri, yaitu refleksi atau pencerminan, khususnya rumus pencerminan terhadap garis y=x. Ada juga beberapa contoh soal yang diberikan agar materi tentang pencerminan ini lebih mudah dipahami.

B. Pengertian Refleksi (Pencerminan)

Seperti disebutkan di atas, salah satu bentuk transformasi geometri adalah pencerminan atau refleksi. Pencerminan sangat mudah dipahami karena dalam keseharian, Kalian juga pasti pernah bercermin. Keduanya memiliki konsep yang sama, yaitu bahwa jarak antara benda dengan cermin akan sama dengan jarak antara bayangan dengan cermin.

Apa yang dimaksud dengan refleksi atau pencerminan? Pencerminan adalah transformasi geometri berupa pemindahan semua titik pada sebuah bidang geometri ke arah sebuah garis atau cermin dengan jarak sejauh dua kali jarak titik-titik pada bidang geometri tersebut terhadap cermin.

Refleksi memiliki dua sifat utama yang wajib Kalian ingat, yaitu:

• jarak titik ke cermin sama dengan jarak bayangan ke titik cermin
• bidang geometri yang direfleksikan sama dengan bayangannya

C. Rumus Pencerminan terhadap Garis y=x dan Contoh Soalnya

Jika digambarkan dalam koordinat kartesius, terdapat empat jenis pencerminan, yaitu pencerminan terhadap titik O (0,0), sumbu x, sumbu y, garis y=x, dan terhadap garis y=-x. Setiap jenis pencerminan memiliki matriks transformasi yang berbeda yang menentukan titik koordinat hasil pencerminan.

Untuk pencerminan terhadap garis y=x, matriks transformasi dan bayangan hasil pencerminannya adalah sebagai berikut.

• Matriks transformasi:

|0  1|

|1  0|

• Bayangan hasil transformasi:

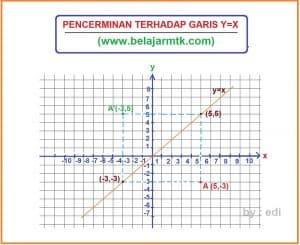
Jika digambarkan dalam koordinat kartesius, pencerminan sebuah titik terhadap garis y=x adalah sebagaimana terlihat pada gambar di bawah ini.

Pencerminan bisa terjadi pada titik maupun garis/kurva. Untuk lebih mudahnya, hasil pencerminan untuk titik dan garis/kurva adalah sebagai berikut.

• Bayangan hasil refleksi sebuah titik:

A(x,y) ——> A'(y,x)

• Bayangan hasil refleksi sebuah garis:

y=f(x) ——> x=f(y)

D. Contoh Soal Pencerminan terhadap Garis y=x

Untuk lebih memahami materi tentang pencerminan terhadap garis y=x, perhatikan contoh soal berikut ini.

• Soal 1

Pada bidang kartesius, terdapat suatu titik yang terletak pada koordinat (5, -3). Tentukan koordinat hasil pencerminannya jika titik tersebut dicerminkan terhadap garis y=x.

Pembahasan:

A(x,y) ——> A'(y,x)

Dengan menggunakan rumus di atas, koordinat hasil pencerminan terhadap garis y=x adalah:

A(5,-3) ——> A'(-3,5)

• Soal 2

Berapakah hasil pencerminan titik (1,5) terhadap garis y=x ?

Pembahasan:

A(x,y) ——> A'(y,x)

Dengan menggunakan rumus di atas, koordinat hasil pencerminan terhadap garis y=x adalah:

A(1,5) ——> A'(5,1)

• Soal 3

Tentukan bayangan garis x=2y+10 terhadap garis y=x.

Pembahasan:

Jika disubstitusikan ke dalam persamaan y=2x+10 akan diperoleh:

y’=2x’+10

x=2y+10

Baca juga : Pengertian Matriks dan Macam-Macam Matriks

Demikianlah pembahasan tentang rumus pencerminan terhadap garis y=x dan contoh soalnya, baik untuk pencerminan terhadap titik maupun garis/kurva. Semoga cukup jelas dan mempermudah Kalian dalam menjawab soal-soal dalam ujian.

Berikut kalkulator rumus pencerminan terhadap Garis y=x, silahkan dicoba.

Click to expand

Terimakasih, semoga bermanfaat.