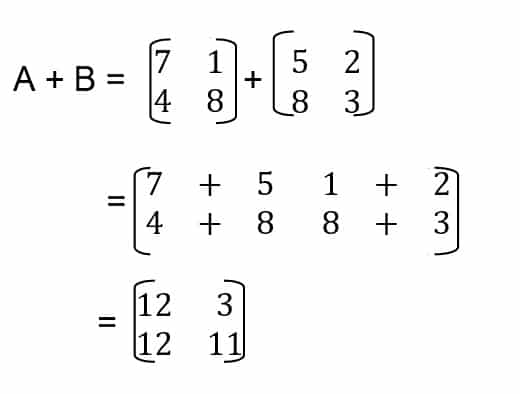Hai sobat Belajar MTK – Ketika belajar matematika saat duduk di bangku SMA pasti akan menemukan bab matriks. Salah satu materi yang nanti dipelajari adalah penjumlahan dan pengurangan matriks beserta contohnya. Meski matematika dianggap sebagai mata pelajaran yang menakutkan, akan tetapi materi ini tidaklah sulit untuk dipelajari.
Perlu diketahui jika materi ini harus dikuasai, terutama penjumlahan dan pengurangan matriks. Sebelum menguasai materi tersebut alangkah lebih baik terlebih dahulu memahami apa itu matriks. Supaya lebih jelas, simak uraian di bawah ini.
A. Pengertian Matriks yang Harus Dipahami
Matriks adalah susunan bilangan (elemen) yang disusun berdasarkan garis dan kolom sehingga berbentuk persegi panjang. Baris dalam matriks merupakan susunan dari bilangan-bilangan yang mendatar. Sedangkan kolom dalam matriks merupakan susunan dari bilangan-bilangan yang tegak.
Perlu diketahui jika matriks dinotasikan menggunakan huruf kapital A, B, K, dan sebagainya. Banyaknya baris dan kolom yang ada di dalam matriks disebut ordo. Sedangkan banyaknya baris dan kolom akan menentukan ukuran dan disebut dengan ordo matriks. Urutan yang harus ingat bahwa baris kemudian kolom. Inilah jenis-jenis matriks juga perlu kamu ketahui.
B. Berikut jenis-jenis matriks :
1. Matriks Nol
Matriks nol adalah salah satu jenis matriks yang semua elemen penyusunnya adalah nol (0). Supaya mudah dipahami alangkah baiknya melihat contoh matriks nol pada gambar di bawah.
2. Matriks Baris
Matriks baris adalah salah satu jenis matriks yang hanya memiliki satu garis. Matriks garis ini bisa dikatakan matriks berordo 1 x n dan dinotasikan sebagai B=[bij]1xn. Contohnya :
3. Matriks Kolom
Matriks kolom adalah salah satu matriks yang hanya memiliki satu kolom. Secara umum matriks jenis ini berordo n x 1 dan dapat dinotasikan sebagai A=[aij]nx1.
Matriks persegi adalah matriks yang berordo n x n atau matriks dengan jumlah baris dan kolom yang sama. Jenis matriks yang satu ini juga disebut dengan matriks persegi berordo n. Contohnya lihat gambar diatas.
1 dan 12 tersebut berada pada diagonal utama B
4. Matriks Identitas
Matriks identitas adalah salah satu jenis matriks konstanta dengan diagonal utamanya adalah 1 dan dinotasikan sebagai I. Matriks identitas memiliki ordo n x n ditulis In. Contohnya lihat gambar diatas.
5. Matriks Skalar
Matriks skalar adalah salah satu jenis matriks yang elemen diagonal utamanya sama. Sedangkan elemen diluar elemen diagonal-nya adalah bernilai nol. Contohnya lihat gambar diatas.
C. Penjumlahan dan Pengurangan Matriks Beserta Contohnya
- Penjumlahan Matriks
Penjumlahan pada matriks ini memiliki syarat dan harus dipenuhi supaya dua buah matriks bisa dijumlahkan. Syarat dua atau lebih matriks bisa dijumlahkan apabila memiliki nilai ordo yang sama. Artinya harus memiliki jumlah baris dan kolom yang sama.
Matriks dengan jumlah baris 3 dan kolom 4 hanya bisa dijumlahkan dengan matriks yang memiliki jumlah baris 3 dan kolom 4. Artinya matriks dengan jumlah baris 3 dan kolom 4 tidak bisa dijumlahkan dengan matriks yang memiliki jumlah baris 4 dan kolom 3.
Kesimpulannya bahwa jumlah baris dan juga kolom antar dua matriks yang akan dijumlahkan harus sama. Supaya lebih mudah dalam memahaminya, perhatikan penjumlahan dua matriks berordo 2×2 berikut ini:
Berikut contoh soal penjumlahan matriks:
Tentukan penjumlahan matriks A dan matriks B
Jawabannya:
- Pengurangan Matriks
Syarat supaya bisa mengurangkan elemen-elemen antar matriks yaitu harus memiliki nilai ordo yang sama. Cara melakukan operasi pengurangan matriks bisa dilihat seperti cara di bawah ini:
A- B = A + (-B)
Cara untuk melakukan operasi pengurangan pada dua matriks tidak jauh berbeda dengan penjumlahan. Supaya lebih jelas, simak contoh pengurangan matriks di bawah ini.
Misalnya
Tentukan: A – B
Jawab :
Baca juga : Rumus Pencerminan terhadap Garis y=x dan Contoh Soalnya
Nah itulah pembahasan materi tentang penjumlahan dan pengurangan matriks beserta contohnya. Diharapkan dengan adanya pembahasan di atas menjadi lebih mudah untuk memahami materi matriks. Serta bisa mengerjakan soal yang diberikan dengan mudah.