Hai sobat Belajar MTK – Materi pelajaran matematika geometri tentang pencerminan terhadap garis x=h dan y=k beserta contohnya akan dibahas dalam artikel berikut ini. Pembahasan tentang materi tersebut diharapkan bisa membantu siswa didik lebih memahami dan bisa mengerjakan soal. Materi yang termasuk dalam kelompok pelajaran matematika geometri tersebut dikenal juga dengan istilah refleksi.
Refleksi atau pencerminan titik yang terdapat pada sebuah bidang datar dimana sifatnya sama seperti bayangan pada cermin datar. Bisa dikatakan juga dalam kalimat yang lebih mudah yaitu refleksi titik akan mempunyai bayangan seperti obyek di depan cermin datar. Sama halnya ketika kita melihat bayangan diri ketika berdiri di depan cermin bedanya hanyalah ini adalah pencerminan titik.
Baca juga : Cara Menggambar Koordinat Kartesius dan Contohnya
Mengawali pembahasan lebih lanjut tentang materi pencerminan titik pada sebuah bidang atau refleksi, sebaiknya ikuti dulu penjelasan di bawah ini.
Refleksi atau Pencerminan Titik Bidang Datar
A. Macam Refleksi Titik Pada Bidang Datar
Sebenarnya di dalam materi tentang pencerminan titik yang terdapat pada bidang datar atau refleksi ada beberapa macam. Meskipun tidak semuanya akan dibahas dalam artikel ini memang sebaiknya siswa mengetahui dulu apa saja macamnya. Refleksi atau pencerminan dalam pelajaran geometri ada jenis yaitu :
- Pencerminan titik terhadap sumbu x
- Pencerminan titik terhadap sumbu y
- Pencerminan titik terhadap sumbu y = k
- Pencerminan titik terhadap sumbu x = h
- Pencerminan pada sumbu pangkal
- Pencerminan titik pada garis x = y
- Pencerminan titik pada garis y = -x
B. Rumus Umum Pencerminan Titik Bidang Datar
Rumus pada pencerminan menurut sumbunya, yaitu :
- Pencerminan pada sumbu x
A(x,y) –> P =A'(x,-y)
- Pencerminan pada sumbu y
A(x,y) –> P =A'(-x,y)
- Pencerminan pada sumbu y = k
A(x,y) –> k =A'(x,2k-y)
- Pencerminan pada sumbu x = h
A(x,y) –> h =A'(2h-x,y)
- Pencerminan pada sumbu pangkal
A(x,y) –> (0,0) =A'(-x,y)
- Pencerminan pada garis x = y
A(x,y) –> y =x =A'(y,x)
- Percerminan pada garis y = -x
A(x,y) –> y =-x =A'(-x,-y)
Dari rumus umum yang dituliskan di atas jelas terlihat bahwa hasil dari pencerminan titik pada bidang datar memang tergantung pada sumbu yang menjadi cerminnya.
Selanjutnya akan kita bahas bagaimana pencerminan terhadap garis x=h dan y=k beserta contohnya agar lebih dipahami oleh siswa atau peserta didik.
1. Pencerminan Titik Terhadap Garis x = h
Menurut rumus yang telah dituliskan pada bagian sebelumnya, pencerminan terhadap garis x = h tidak jauh berbeda dengan macam refleksi lainnya. Berikut ini akan diberikan contoh dari pencerminan titik terhadap garis x = h seperti yang dimaksud.
Rumus Pencerminan pada sumbu x = h
A(x,y) –> h =A'(2h-x,y)
Keterangan :
- A adalah titik A pada bidang datar
- A’ adalah titik A setelah pencerminan
- x adalah titik yang terdapat pada sumbu x
- y adalah titik yang terdapat pada sumbu y
- h adalah bilangan yang berasal dari sumbu x
- x : h adalah hasil pencerminan titik pada sumbu x = h
Contoh Soal :
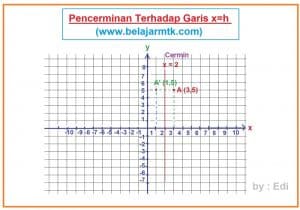
Berapakah hasil pencerminan titik (3,5) pada sumbu x = h = 2
Jawaban :
x = 3; y = 5
A(x,y) –> x:h = A’(2h-x, y)
A(3,5)–> x:2 = A’( 2.2-3, 5)
= A’ (1,5)
2. Pencerminan Titik Terhadap Garis y = k
Pembahasan selanjutnya yaitu pencerminan terhadap garis y = k, seperti berikut ini.
Pencerminan pada sumbu y = k
Keterangan :
- A adalah titik A pada bidang datar
- A’ adalah titik A setelah pencerminan
- x adalah titik yang terdapat pada sumbu x
- y adalah titik yang terdapat pada sumbu y
- k adalah bilangan yang berasal dari sumbu y
- y : k adalah hasil pencerminan titik pada sumbu y = k
Contoh Soal :
Berapakah hasil pencerminan titik (3,5) pada sumbu y = k= 2
- Jawaban :
x = 3; y = 5
A(x,y) –> y:k = A’(x, 2k- y)
A(3,5)–> x:-2 = A’(3, 2(2) – 5)
= A’ (3,-1)
Baca juga : Pencerminan Terhadap Sumbu X dan Sumbu Y Contohnya
Demikian penjelasan tentang pencerminan terhadap Garis x=h dan y=k beserta contohnya semoga bermanfaat.
Berikut kalkulator rumus pencerminan terhadap Garis x=h dan y=k, silahkan dicoba.
Terimakasih, semoga bermanfaat.