Hai sobat Belajar MTK – Ada yang belum tahu mengenai rumus integral dasar dan contoh soalnya? Atau mungkin sudah tahu, tetapi belum begitu paham mengenai rumus integral dasar? Nah, berikut ini adalah penjelasan mengenai rumus integral dasar dan juga beberapa contoh soalnya.
A. Rumus Integral Dasar dan Contoh Soalnya
Pengertian Integral secara sederhana adalah invers atau kebalikan dari suatu turunan. Penjabaran lebih luasnya adalah sebuah konsep bentuk penjumlahan berkesinambungan dan juga bersama dengan inversnya.
Ide integral sendiri muncul ketika matematikawan memikirkan bagaimana caranya menyelesaikan masalah yang berkebalikan dengan solusi diferensiasi.
B. Jenis-Jenis Integral
Berdasarkan pengertian integral, terdapat dua hal yang dilakukan di dalamnya hingga dikategorikan menjadi 2 jenis.
- Yang pertama adalah integral sebagai invers/kebalikan dari turunan, disebut juga sebagai integral tak tentu.
- Yang kedua adalah integral sebagai limit dari jumlah atau suatu luas daerah tertentu disebut sebagai integral tentu.
Baca juga : Rumus Mencari Determinan Matriks dan Contohnya
1. Integral Tak Tentu
Integral tak tentu merupakan bentuk integral yang hasilnya berupa fungsi dalam variabel tertentu, di mana variabel tersebut masih memuat konstanta integrasi.
Oleh karena itu, rumus umum integral tak tentu dinyatakan dalam formula sebagai berikut ini.

2. Integral Tentu
Pada bahasan yang sebelumnya, telah dibahas mengenai integral tak tentu, di mana hasil dari integrasi tersebut masih berupa fungsi.
Sedangkan jika hasil integrasinya berupa nilai tertentu, integral tersebut bernama integral tentu. Bentuk umum dari integral tentu adalah sebagai berikut ini.

C. Aplikasi Integral Tentu
Bukan hanya perlu mengetahui rumus integral dasar dan contohnya, kita juga harus tahu kalau integral bisa diaplikasikan dalam kehidupan sehari-hari.
Salah satu contoh yang umum dikenal adalah penggunaan integral tentu untuk menghitung luas daerah.
Luas daerah yang dimaksud adalah luas daerah di bawah kurva. Namun, ada beberapa hal yang harus dilakukan untuk menghitung integral tentu seperti berikut ini.
- Batas daerah yang akan diintegralkan haruslah jelas. Batas daerah yang dimaksud adalah batas kiri dan kanan serta batas atas dan bawahnya.Bentuk batas daerah bisa berupa fungsi atau konstanta, fungsi linier dan nonlinier. Jika salah satu batas belum diketahui, maka batas tersebut harus dicari terlebih dahulu supaya luasnya bisa dihitung.
- Kita harus mampu menggambar daerah di dalam kurva sesuai dengan batas-batas yang telah ditentukan. Karenanya, diperlukan kemampuan untuk menggambar dengan baik. Jika tidak bisa menggambar dengan baik, maka paling tidak menggambar sesuai dengan ukuran bidang yang digambar.
- Menempatkan rumus yang tepat untuk menghitung luas daerah berdasarkan ketentuan yang telah ada. Perhatikan gambar daerah dan rumus yang bersesuaian. Namun jangan terlalu khawatir, setiap daerah memiliki rumus dan fungsinya masing-masing.
D. Contoh Soal Integral
- Contoh soal 1
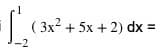
Pembahasan
Penjelasan dari soal no 1 tersebut adalah sebagai berikut. Batas atas dalam soal ini adalah 1. Sedangkan batas atas dalam soal adalah -2. Tahap pertama yang perlu dilakukan dalam integral ini adalah melakukan integral fungsi 3x2 + 5x + 2 menjadi seperti di bawah ini.
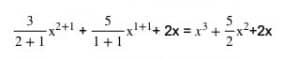
Setelah mendapatkan bentuk integral dari fungsi tersebut, maka kita harus lanjut ke langkah selanjutnya.
Langkah selanjutnya adalah dengan memasukkan nilai batas atas dan bawah ke dalam fungsi tersebut. Kemudian mengurangkannya menjadi seperti berikut.
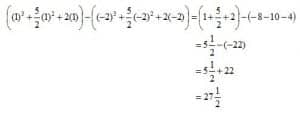
Setelah semua langkah dilakukan dengan benar, maka kita akan mendapatkan sebuah hasil akhir.
Hasil dari integral tersebut adalah 27,5. Jika hasilnya bukan 27,5 berati ada kesalahan dalam proses penghitungan. Cermati ulang penghitungan dari awal untuk melihat bagian yang salah.
- Tentukanlah integral x jika f’(x) = 3x2
Pembahasan
Dalam mengerjakan soal ini, ada beberapa hal yang harus diperhatikan. Salah satunya adalah memperhatikan fungsi dengan seksama.
Dalam soal ini fungsi berbentuk f’(x) yang menandakan bahwa fungsi tersebut merupakan turunan dari fungsi tertentu. Untuk mengerjakannya, kita dapat menggunakan sifat dasar integral tak tentu seperti di bawah.
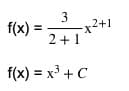
Hasil dari nilai integral tersebut adalah x3+c. Jika hasilnya berbeda, maka perlu untuk memperhatikan kembali proses penghitungan karena memang integral ini membutuhkan perhatian lebih pada fungsinya. Jika fungsi salah dalam penempatannya, maka hasil akhirnya pasti salah.
- Tentukanlah integral x jika diketahui g’(x) = 3x5+3
Pembahasan
Untuk mengerjakan soal di bawah ini, kita dapat menggunakan sifat seperti soal pertama. Dalam soal ini, g’(x) merupakan turunan dari suatu fungsi.
Baca juga : Pengertian Statistika Fungsi Jenis dan Rumusnya
Berikut ini adalah cara penyelesaiannya. Pastikan hasil akhirnya dari g’(x) adalah g(x) = 1/2 x6 + 3x + C.
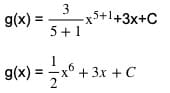
Demikian penjelasan singkat rumus integral dasar dan contoh soalnya. Semoga dengan membaca ulasan ini, soal-soal integral akan lebih mudah diselesaikan.

