Hai sobat Belajar MTK – Karena banyak digunakan dalam menyelesaikan persoalan matematika, pengertian matriks dan macam-macam matriks sangat penting untuk dipahami. Matriks sangat berguna untuk mencari solusi persamaan linear dan transformasi liner, seperti rotasi dalam 3 dimensi. Oleh karena itu, simak baik-baik penjelasan lengkap tentang definisi dan jenis-jenis matriks di bawah ini.
1. Pengertian Matriks
Matriks didefinisikan sebagai sekelompok bilangan di dalam sebuah jajaran berbentuk persegi panjang yang diatur berdasarkan baris dan kolom serta terletak di antara dua tanda kurung. Fungsi tanda kurung adalah untuk mengapit susunan anggota matriks. Bentuk tanda kurung bisa berupa kurung biasa maupun kurung siku.
Bilangan pada matriks disebut unsur atau elemen matriks. Berdasarkan susunannya, kumpulan elemen matriks dibedakan menjadi dua macam, yaitu
- baris: kumpulan elemen matriks yang tersusun secara mendatar (horizontal)
- kolom: kumpulan elemen matriks yang tersusun secara tegak (vertikal).
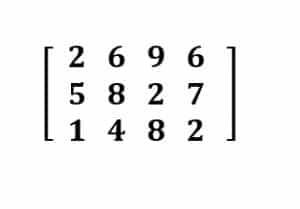
Selain baris dan kolom, di dalam matriks, dikenal juga istilah ‘ordo’. Ordo matriks adalah bilangan yang menunjukkan jumlah baris (m) dan kolom (n) yang ada pada matriks tersebut. Sebuah matriks biasanya ditulis menggunakan huruf kapital dan tebal. Matriks yang mempunyai m baris dan n kolom disebut dengan matrik m x n dan dinamakan matriks dengan ordo m x n. Contoh matriks dengan ordo (4×3) adalah sebagai berikut.
2. Macam-Macam Matriks
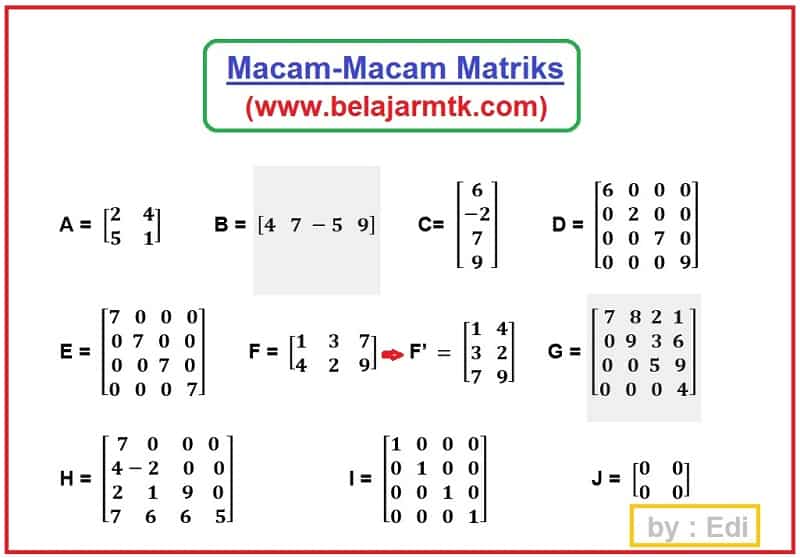
Dalam ulasan tentang pengertian matriks dan macam-macam matriks ini, kita akan mengenal 10 macam matriks, yaitu matriks persegi, baris, kolom, diagonal, skalar, transpose, segitiga atas dan bawah, identitas, dan matriks nol. Apa yang dimaksud dengan matriks-matriks tersebut, berikut penjelasannya.
A . Matriks Persegi
Matriks persegi adalah matriks yang mempunyai jumlah baris dan jumlah kolom yang sama. Jadi, matriks persegi secara umum berordo n x n. Contoh matriks persegi pada gambar dibawah abjad A.
B . Matriks Baris
Matriks baris adalah matriks yang hanya memiliki satu baris dan biasanya berordo 1 x n. Contoh matriks baris pada gambar diabawah abjad B.
C. Matriks Kolom
Matriks kolom adalah matriks yang hanya terdiri dari satu kolom sehingga disebut matriks berordo m x 1. Contoh matriks kolom adalah sebagai berikut abjad C.
D. Matriks Diagonal
Matriks diagonal juga merupakan matriks persegi. Akan tetapi, pada matriks diagonal, seluruh elemennya adalah nol, kecuali elemen pada diagonal utamanya. Untuk lebih jelasnya, berikut contoh elemen diagonal gambar diatas D.
E. Matriks Skalar
Matriks skalar adalah matriks yang diagonal utamanya terdiri dari elemen yang sama, sedangkan elemen lainnya adalah nol seperti contoh diatas E.
F. Matriks Transpose
Matriks transpose A yang berordo m x n dinotasikan sebagai A’ dan memiliki ordo n x m. Jadi, baris pada matriks A menjadi kolom pada matriks transpose A’. Agar lebih jelas, perhatikan contoh gambar diatas yang F.
G. Matriks Segitiga Atas
Matriks segitiga atas berasal dari matriks persegi yang seluruh elemen di bawah diagonal utamanya adalah nol. Berikut contoh matriks segitiga atas pada gambar G
H. Matriks Segitiga Bawah
Berkebalikan dengan matriks segitiga atas, pada matriks segitiga bawah, seluruh elemen yang terletak di atas diagonal utamanya adalah nol. Berikut contoh matriks segitiga bawah gambar H.
I. Matriks Identitas
Matriks identitas adalah matriks yang seluruh elemen diagonal utamanya adalah 1 dan elemen lainnya 0. Pada umumnya, matriks identitas dinotasikan dengan huruf I. Contohnya dapat dilihat di diatas gambar I.
J. Matriks Nol
Matriks nol adalah matriks yang semua elemen pada matriks adalah bilangan nol. Contohnya diatas gambar J.
Demikianlah ulasan mengenai pengertian matriks dan macam-macam matriks dalam matematika. Sebagai tambahan, matriks juga memiliki beberapa operasi matematika, yaitu penjumlahan, pengurangan, dan perkalian dengan skalar.