Pengertian dan Sifat Bilangan Berpangkat Beserta Contoh Soalnya

Hai sobat Belajar MTK – Di dalam matematika, bilangan yang memiliki pangkat terdiri dari bilangan dengan pangkat bulat positif (bilangan asli), pangkat bulat negatif, pangkat nol, pangkat rasional dan pangkat riil. Notasi pangkat digunakan untuk menuliskan hasil kali dari suatu bilangan berulang dalam bentuk yang lebih sederhana. Seperti misalnya, kita memiliki tiga faktor a yang sama, sehingga dapat menggunakan lambang a³ untuk menyatakan (a x a x a), dengan 3 dituliskan di sebelah kanan atas a adalah yang dinamakan pangkat dari a dan menyatakan banyaknya faktor a yang terulang, dapat ditulis

a³ = a x a x a

Bilangan berpangkat yang paling banyak dibahas antara lain adalah bilangan berpangkat positif, bilangan berpangkat negatif dan bilangan berpangkat nol. Untuk lebih jelasnya, kami akan bahas satu per satu pengertian dan sifat-sifat dari ketiga bilangan berpangkat tersebut.

Baca juga : Pembulatan Bilangan Desimal Puluhan dan Ratusan Terdekat

• Bilangan Berpangkat Positif

Bilangan berpangkat positif adalah bilangan yang mempunyai pangkat atau eksponen positif. Bilangan berpangkat positif memiliki sifat-sifat tertentu, di mana terdiri dari a, b, bilangan real m, n, yang adalah bilangan bulat positif. Sifat-sifat bilangan berpangkat positif antara lain sebagai berikut:

• Sifat-Sifat Bilangan Berpangkat Positif

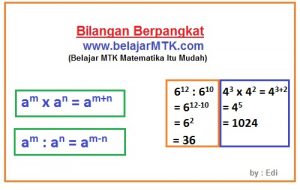
a^m x aⁿ = a^m+n

a^m : aⁿ = a^m-n, untuk m > n 

(a^m)ⁿ = a^mn

(ab)^m = a^mb^m

(a/b)^m = a^m/b^m, untuk b ≠ 0

• Bilangan Berpangkat Negatif

Tidak semua bilangan berpangkat memiliki nilai positif, beberapa di antaranya adalah bilangan bulat negatif. Untuk bilangan berpangkat negatif berlaku sifat sebagai berikut:

a^-n = 1/aⁿ atau aⁿ = 1/a^-n

• Bilangan Berpangkat Nol

Jika a ∈ R, a ≠ 0, dan n merupakan bilangan bulat negatif, maka

Selain bilangan berpangkat positif dan bilangan negatif, dalam matematika juga terdapat bilangan berpangkat nol. Sebelumnya kita telah mengetahui bahwa aⁿ/aⁿ=1 . Berdasarkan sifat pembagian bilangan berpangkat positif dapat diperoleh aⁿ/aⁿ = a^n-n, maka a⁰ = 1 . Sehingga sifat untuk bilangan berpangkat nol adalah jika a bilangan riil dan a tidak sama dengan 0, maka a⁰ = 1.

• Contoh Soal

Soal 1:

Hasil Perkalian dari 4³ x 4² adalah . . .
A. 1028
B. 1024
C. 120
D. 96

Penyelesaian:

Apabila bilangan yang dipangkatkan sama, maka cara penyelesaiannya sangatlah sederhana yaitu:

4³ x 4² = 4³⁺²
= 4⁵
= 1024
Jawaban: B

Soal 2:

Hasil perkalian dari 27^1/3 x 4^3/2 adalah . . .
A. 24
B. 26
C. 28
D. 18

Penyelesaian:

Karena pangkat dari bilangan tersebut tidak sama maka kita perlu menyederhanakan bilangan yang berpangkat itu terlebih dahulu.

= 3¹ x 2³
= 3 x 8
= 24

Jawaban: A

Soal 3

Bentuk sederhanakan dari hasil pembagian 6¹² : 6¹⁰ adalah . . .
A. 6^1/2
B. 6^6/5
C. 6²

D.6³

Penyelesaian:

Untuk soal pembagian, bilangan yang dapat kita sederhanakan hanya apabila bilangan yang dipangkatkan itu sama. Jadi, apabila bilangan yang dipangkatkan tidak sama maka tidak dapat dipangkatkan.

Karena nilai bilangan yang dipangkatkan sama maka cara penyelesaiannya yaitu:

⇔  6¹² : 6¹⁰ 
= 6^12-10
= 6²
Jawaban: C

Soal 4

Hasil dari 9^6/3 adalah . . .
A. 32
B. 9
C. 27
D. 81

Penyelesaian:

9^6/3 = 3 ^{2 x 6/3}
= 3⁴
= 81

Atau dengan cara cepatnya yaitu sebagai berikut:

9^(6/3) = 9²
= 81

Jawaban: D

Berikut kalkulator hitung perkalian dan pembagian bilangan berpangkat

Baca juga : Pengertian Relasi dan Fungsi dengan Contoh Soalnya

Advertisements

Demikian ulasan kami mengenai pengertian dan sifat Bilangan Berpangkat beserta contoh soalnya. Semoga bermanfaat.