Hai Sobat Belajar MTK – Selain bangun datar, di matematika juga ada bangun ruang. Bangun ruang sering disebut juga bangun tiga dimensi. Ada banyak sekali jenis bangun ruang tiga dimensi di sekitar kita, salah satunya adalah kubus. Kubus ini sering kita jumpai dalam kegiatan sehari-hari seperti pada kursi, lemari, kotak dan lain sebagainya.
Selain luas permukaan, bangun ruang juga mempunyai volume di dalamnya. Berikut ini rumus volume kubus dan luas permukaan kubus lengkap contoh soalnya, untuk mempermudah Anda atau siswa dalam pembelajarannya. Yuk tunggu apalagi, simak informasi berikut ini.
Pengertian dan Sifat-Sifat Kubus
A. Pengertian Kubus
Sudah disampaikan di atas kubus merupakan bangun ruang tiga dimensi yang dibatasi dengan 6 bidang sisi berbentuk bujur sangkar yang kongruen. Kubus juga sering disebut dengan bidang 6 beraturan. Bukan hanya itu saja, kubus juga bentuk khusus dalam prisma segiempat.
B. Sifat-sifat Kubus
- Kubus mempunyai 6 sisi/bidan berbentuk persegi dengan ukuran luas yang sama, yaitu sisi : ABCD, EFGH, ABFE, CDHG, BCGF dan ADHE
- Kubus mempunyai 12 rusuk dengan ukuran yang sama panjang, yaitu rusuk : AB, BC, CD, DA, EF, FG, GH, HE, AE, BF, CG dan DH
- Kubus mempunyai 8 buah titik sudut (titik perpotongan antara 2 rusuk), yaitu : A, B, C, D, E, F, G, dan H
- Kubus mempunyai 12 diagonal sisi atau diagonal bidang, yaitu : AF, BE, DG, CH, AC, BD, FH, EG, BG, CF, DE dan AH
- Kubus mempunyai 4 buah diagonal ruang (ruas garis penghubung 2 titik sudut di dalam ruang kubus yang saling berhadapan), yaitu : AG, BH, CE dan DF
- Kubus mempunyai 6 buah bidang diagonal (bidang yang terbentuk akibat 2 buah rusuk yang sejajar di dalam ruang bangun), yaitu : ABGH, CDEF, ADGF, BCHE, BDHF, ACGE
Rumus Volume Kubus dan Luas Permukaan Lubus Lengkap Contoh Soalnya

Rumus Kubus
- Luas Permukaan Kubus
L = 6 x S2
- Volume Kubus
V = S3
S = panjang sisi = rusuk
C. Contoh Soal dan Pembahasan
- Contoh Soal 1
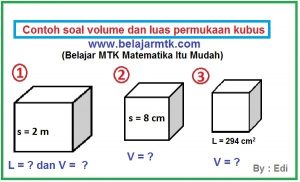
Hitung volume dan luas permukaan box yang mempunyai panjang dan lebar sama yaitu 2 m !
Jawaban :
Volume box
V = S3
V = 23
V = 8 m3
Luas Permukaan box
L = 6 x S2
L = 6 x 22
L = 24 m2
Jadi, volume dan luas permukaan box adalah 8 m3 dan 24 m2
- Contoh Soal 2
Tentukan volume kubus yang memiliki rusuk sepanjang 8 cm!
Jawaban :
Volume Kubus
V = S3
V = 83
V = 512 cm3
- Contoh Soal 3
Sebuah kubus mempunyai luas permukaan sebesar 294 cm2, tentukan volume kubus tersebut !
Jawaban :
Langkah pertama mencari panjang sisi
Luas permukaan = 6 x S2
L = 6 x S2
294 = 6 x S2
S2 =294 / 6
S = √49
S = 7 cm
Volume Kubus
V = S3
V = 73
V = 343 cm3
- Contoh Soal 4
Sebuah kubus mempunyai panjang 15 cm. Jika kubus tersebut dipotong menjadi kubus kecil-kecil dengan panjang rusuk 5 cm, berapakah jumlah kubus yang terbentuk
Jawaban :
Volume kubus besar
V = S3
V = 153
V = 3.375 cm3
Volume kubus kecil
V = 53
V = 125 cm3
Jadi jumlah kubus yang terbentuk adalah V besar : V kecil = 3.375 cm3 : 125 cm3 = 27 buah.
- Contoh Soal 5
Sebuah wadah berbentuk kubus mempunyai volume sebesar 512 cm3, berapakah panjang wadah tersebut?
Jawaban :
V = S3
512 cm3 = S3
S = 3√512
S = 8 cm
Jadi panjang wadah tersebut adalah 8 cm
- Contoh Soal 6
Andi mempunyai kado berbentuk kubus dengan panjang rusuk 20 cm, berapa luas kertas yang dibutuhkan untuk membungkus kado milik Andi tersebut?
Jawaban :
Luas permukaan kado
L = 6 x S2
L = 6 x 202
L = 2400 cm2
Jadi, luas kertas yang dibutuhkan untuk membungkus kado adalah 2.400 cm2.
- Contoh Soal 7
Tentukan luas permukaan kubus yang mempunyai volume sebesar 8.000 cm3!
Jawaban :
Langkah pertama mencari panjang rusuk
V = S3
8.000 = S3
S = 3√8000
S = 20 cm
Luas permukaan kubus
L = 6 x 202
L = 2400 cm2
Kubus merupakan bangun ruang yang paling sering dijumpai di sekitar kita. Hampir semua barang di dekat kita mempunyai bentuk kotak atau kubus. Untuk itu Anda pasti tidak asing dengan bangun ruang 3 dimensi ini. Terlebih lagi materi ini sudah diajarkan sejak sekolah dasar. Untuk Anda yang masih bingung mengenai kubus dan rumus-rumusnya, silahkan baca dan pahami beberapa contoh soal diatas.
Berikut kumpulan rumus-rumus kubus
| Dicari | Rumus | Keterangan |
| Volume | V = S3 | |
| Luas | L = 6 x S2 | |
| Sisi | s = 3√V | diketahui V |
| Sisi | s = √L/6 | diketahui L |
| Diagonal sisi | ds = s √2 | |
| Diagonal ruang | dr = s √3 | |
| Luas Bidang Diagonal | Lbd = s x s √2 |
Berikut kalkulator hitung volume kubus dan luas permukaan kubus, silahkan dicoba.
Baca juga : Rumus Luas Trapesium dan Keliling Trapesium Lengkap Contoh Soalnya
Itulah tadi sedikit pembahasan mengenai rumus volume kubus dan luas permukaan kubus lengkap contoh soalnya. Sangat mudah untuk mencari luas dan volume kubus atau balok, yang terpenting Anda sudah mengetahui berapa panjang rusuk kubus tersebut. Mudah bukan? Jika Anda mempelajarinya berulang-ulang, pasti akan terasa mudah. Semoga informasi di atas bermanfaat untuk Anda semua. Semangat belajar dan capai nilai yang memuaskan.

Satu pemikiran pada “Rumus Volume Kubus dan Luas Permukaan Kubus Lengkap Contoh Soalnya”